lamechang-dev

Webフロントエンドエンジニア lamechangのブログ。

【アルゴリズム】【動的計画法】ナップザック問題のアルゴリズム実装

C++ アルゴリズム

動的計画法とは

アルゴリズム分類の１つ。与えられた問題全体を一連の部分問題として分解した上で、それぞれの部分問題に対する解をメモ化しながら、小さな部分問題から大きな部分問題へと順に計算 => 解を求めていく手法のことを指します。動的計画法を適用できるようなケースは非常に多く、解法パタンの中には特殊なテクニックを要するものも存在します。

動的計画法を用いることで解を用いることができる問題の代表例は以下の通りです。
- ナップザック問題
- スケジューリング問題
- 発電計画問題

今回は、動的計画法の理解をする上で典型パターンといてよく用いられるナップザック問題のアルゴリズム実装をします。

ナップザック問題とは

ナップサックの中にいくつかの品物を詰め込み入れた品物の総価値を最大にするという問題を指します。より一般化して、以下のような命題を考えます。

N個の品物があり， i(＝0,1,...,N－1)番目の品物の重さは weight_i，価値は value_iで与えられます。 この N個の品物から，重さの総和が Wを超えないように，いくつか選びます。 選んだ品物の価値の総和として考えられる最大値を求めてください(ただし， Wや weight_iは０以上の整数とします)．

動的計画法における部分問題の考え方は、以下のことを意識しながら部分問題を構成することで、部分問題同士の遷移を考察し、数式に落とし込むことで解法を導くことができます。

部分問題の作り方の基本パターンは
N個の対象物{0,1,...,N－1}に関する問題に対して，最初のi個の対象物{0,1,...,i－1}に関する問題を部分問題として扱い、一般化する
ということになります。

なので、この基本パターンを上記の命題にも適用してみるとしましょう。

部分問題の適用

以下のような部分問題を考えることができます。

ans[i] = 最初のi個の品物{0,1,...,i－1}までの中から重さがWを超えないように選んだときの，価値の総和の最大値

こうした場合の部分問題同士の遷移を考えてみます。

ans[i] から ans[i+1] に遷移する場合、 i番目の品物を選択するか否かの２通りが考えられます。しかし命題をちゃんと確認してみると重さの総和が Wを超えないようにという条件がありますが、こちらの条件を満たすか否かの判断が上記の部分問題だけでは分かりません。よって、部分問題の ans[i] を決定づける要素に、重さwを付け加えてやることにします。

ans[i][w] = 最初のi個の品物{0,1,...,i－1}までの中から重さがwを超えないように選んだときの，価値の総和の最大値

こうすることで、選択肢のグループを決定づける変数にwが加わりました。この状態で、グループごとの遷移を表現できるか考えてみます。以下において、dp[i][w](w＝0,1,...,W)の値が求まっている状態を仮定した上で、dp[i+1][w](w＝0,1,...,W)を求めていくことを考えてみます。

i番目の品物を選ぶとき

選んだ後の価値の総和ans[i+1][w]に対し、選ぶ前の価値の総和は ans[i][w - weight[i]]となります。 また、その選ぶ前の状態の価値の総和から value[i+1]が加わることを考えると、

ans[i+1][w] は ans[i][w - weight[i]] + value[i] と表現することができることがわかります。よって、ans[i+1][w] と ans[i][w - weight[i]] + value[i] の間の最大値を求めればいいことがわかります。

ただし、w - weight[i]>=0 の場合のみ適用できることに注意します。

i番目の品物を選ばないとき

選ばなかった後の価値の総和をans[i+1][w]に対し、選ばなかった前は重さが変わるはずがないので価値の総和はans[i][w]です。よって、ans[i+1][w] と ans[i][w] の間の最大値を求めてあげればいいことがわかります。

具体例で遷移を確認

ここで、この遷移をより具体的に考えてみます。このような状況を考えてみましょう。品物が４個で、(weight,value)＝{(2,3),(1,2),(3,6),(2,1)} 実際のans[i][w]を以下のマス目状の図に埋めていきます。

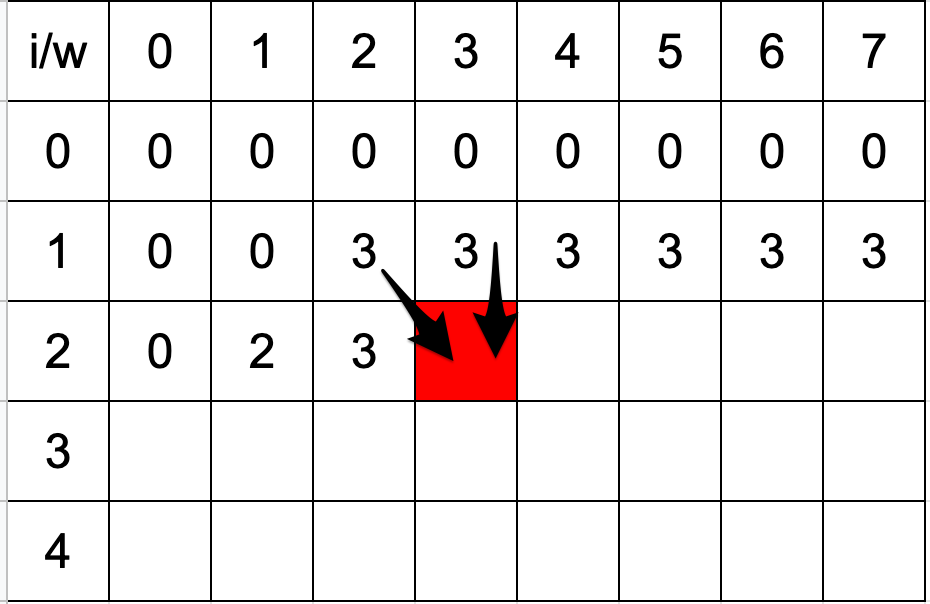
先ほど紹介した遷移を利用していきこの表を左上から埋めていくことを考えた時に、赤マスで表現されるans[3][3] の値の算出は以下のように行われます。

  1. 2番目の品物を選んだ場合は、ans[2][3 - weight[2]] + value[2] = ans[2][2] + 2 = 3 + 2 = 5

  2. 2番目の品物を選ばない場合は、ans[2][3] = 3

と計算されます。

仮に、それぞれのマスがまず０で初期化されていると前提を置くとなると、この２パターンによって算出される値の最大値がans[3][3]の最終解になっていることがイメージできるのではないでしょうか。

また、アルゴリズムの計算量自体は、それぞれのグループにおける計算量が O(1)であり、グループの個数は NWだけ存在しますので、 全体で O(NW)で表現されます。

C++ でのアルゴリズム実装

以下のようになります。

#include <iostream>
#include <stdio.h>
#include <vector>
using namespace std;

template<class T> void chooseMax(T& a, T b) {
  if (a < b) {
    a = b;
  }
}

int main() {

  int N; long long W;
  cin >> N >> W;
  vector<long long> weight(N), value(N);
  for (int i = 0; i < N; i++)
  {
    cin >> weight[i] >> value[i];
  }

  // アンサーテーブル定義
  vector<vector<long long> > ans(N + 1, vector<long long>(W + 1, 0));

  for (int i = 0; i < N; i ++) {
    for (int w = 0; w <= W; w ++) {
      if (w - weight[i] >= 0) {
        chooseMax(ans[i + 1][w], ans[i][w - weight[i]] + value[i]);
      }

      chooseMax(ans[i + 1][w], ans[i][w]);
    }
  }

  cout << ans[N][W] << endl;
}